lm関数の使い方～近似直線の式(y=ax+b)を作る関数～【R備忘録】

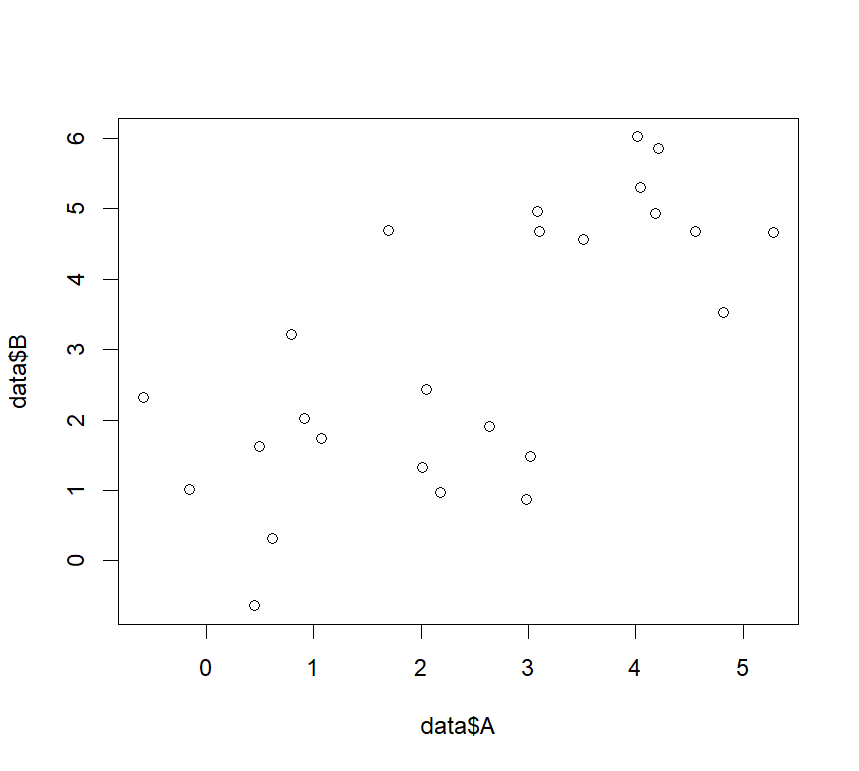
上記の変数Aと変数Bの関係を知りたい！

そんな時「y=ax+b」の関係式に近似し、その直線を描くことは一つの鉄板だと思います。

その近似直線の式を作るために、回帰分析を行う関数であるlm関数について、本記事では紹介します。

そのほかの【R備忘録】はこちら

Rの参考書の購入はこちらから

基本的な使い方
重回帰分析の場合
終わりに

基本的な使い方

lm関数の基本的な使い方は、「lm(目的変数～説明変数,data=データフレーム名）」です。

#例）データフレーム"data"に格納されている変数Aと変数Bの関係を知りたいとき
lm(B～A,data=data）
lm1<-lm(B～A,data=data）#このように回帰分析の結果を変数に格納すると便利です。

この関数を入力すると、近似直線の式の切片（すなわち”ｂ”の部分）と傾き（すなわち”a”の部分）の値が出力されます。
また、summary(回帰分析の結果を格納した変数)と入力することにより、その結果の詳細を見ることができます。

lm(B~A,data=data)

Call:
lm(formula = B ~ A, data = data)

Coefficients:
(Intercept)            A  
     1.0343       0.7976  #切片(Intercept)と傾き　　

> summary(lm(B~A,data=data))

Call:
lm(formula = B ~ A, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.5352 -1.2327  0.1004  1.1690  2.3006 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1.0343     0.5089   2.032 0.053831 .  
A             0.7976     0.1733   4.604 0.000125 *** 
#それぞれの推定値(Estimate)、標準誤差(Std. Error)、t値(t value)、p値(Pr(>|t|))
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.417 on 23 degrees of freedom　#残差の標準誤差と自由度
Multiple R-squared:  0.4796,	Adjusted R-squared:  0.4569 #R二乗値
F-statistic: 21.19 on 1 and 23 DF,  p-value: 0.000125　#F値とp値

この関係を図示したい場合は、plot関数で二つの変数の散布図を描いた後、”abline(回帰分析の結果を格納した変数)”と入力することにより、出力することができます。
—plot関数の使い方

plot(data$A,data$B)
abline(lm1)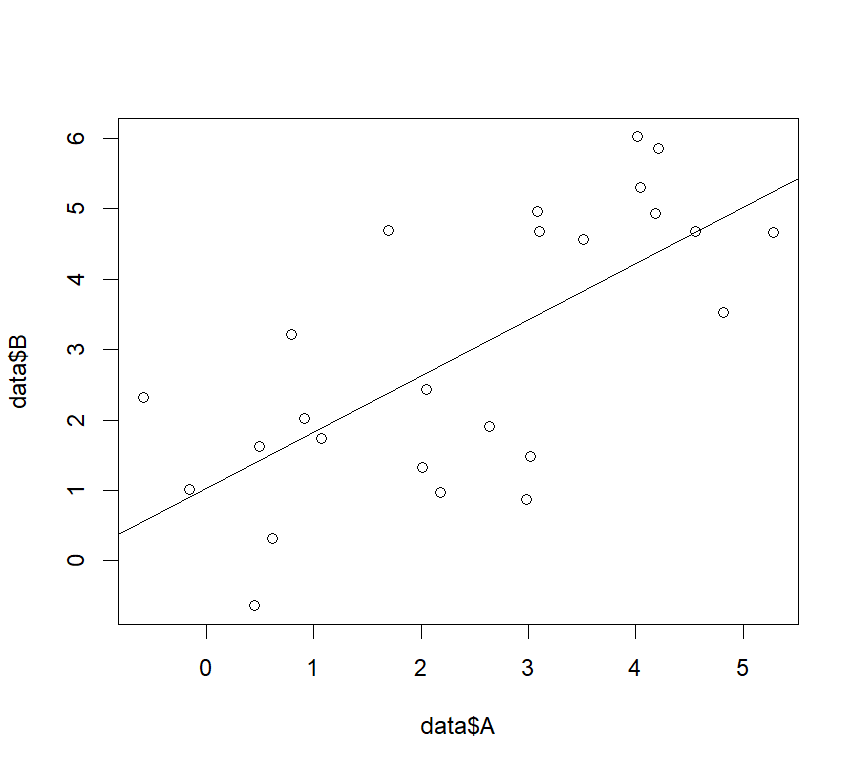

重回帰分析の場合

説明変数が二つ以上になる重回帰分析もこのlｍ関数を用いることにより解析することができます。
たとえば、ｘとｙの二つのグループに分かれた、変数Ａと変数Ｂの関係について重回帰分析してみます。

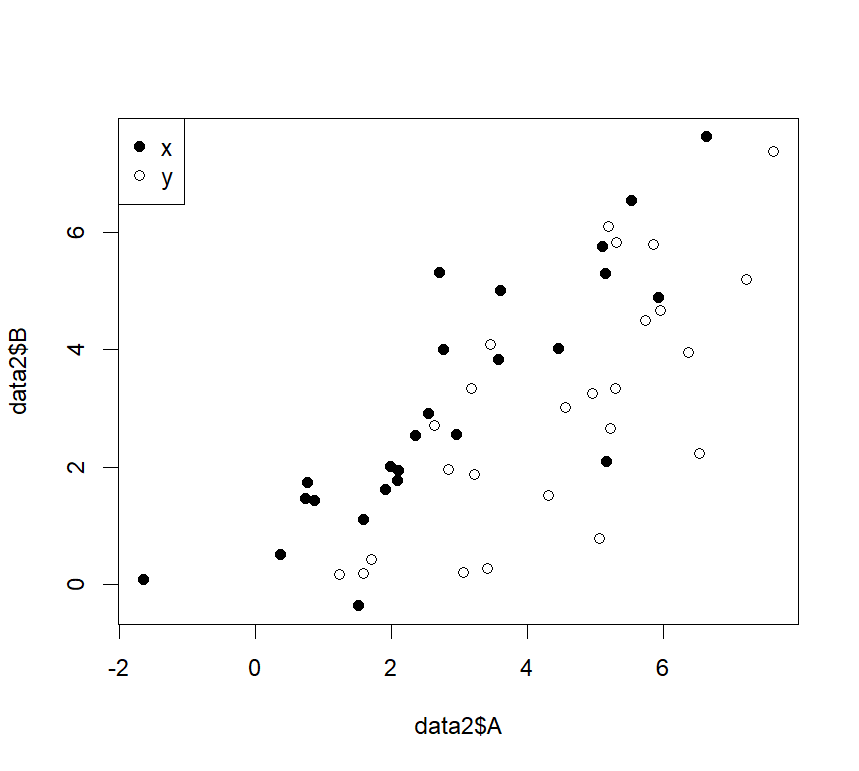
重回帰分析でも基本的な使い方は同じで、右のように入力します「lm(目的変数～説明変数１＋説明変数２,data=データフレーム名）」。

#例）データフレーム"data2"に格納されている変数Aと変数Bの関係とそのグループ間の違いを知りたいとき
lm(B~A+group,data=data2)
lm2<-lm(B~A+group,data=data2)）#このように回帰分析の結果を変数に格納すると便利です。

この関数を入力すると、先ほどと同様に、近似直線の式の切片（すなわち”ｂ”の部分）と傾き（すなわち”a”の部分）の値が出力されます。
また、summary(回帰分析の結果を格納した変数)と入力することにより、その結果の詳細を見ることができます。

> lm(B~A+group,data=data2)

Call:
lm(formula = B ~ A + group, data = data2)

Coefficients:
(Intercept)            A       groupY  
     0.5331       0.8818      -1.4503 

> summary(lm(B~A+group,data=data2))

Call:
lm(formula = B ~ A + group, data = data2)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.99478 -0.59243 -0.05263  0.93442  2.44286 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.53308    0.37852   1.408 0.165618    
A            0.88183    0.09829   8.972 9.42e-12 ***
groupY      -1.45034    0.39652  -3.658 0.000642 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.282 on 47 degrees of freedom
Multiple R-squared:  0.6313,	Adjusted R-squared:  0.6157 
F-statistic: 40.25 on 2 and 47 DF,  p-value: 6.54e-11