二項検定とは
二項検定とはある二つのカテゴリーに分けられるデータの比率が、理論上の分布から有意に偏っているかを、二項分布を用いて調べる統計学的検定のことです。
本検定の帰無仮説と対立仮説は以下の通りです。
1.帰無仮説:二つのカテゴリーの比率は理論上の比率である。
2.対立仮説:二つのカテゴリーは理論上の比率ではない。
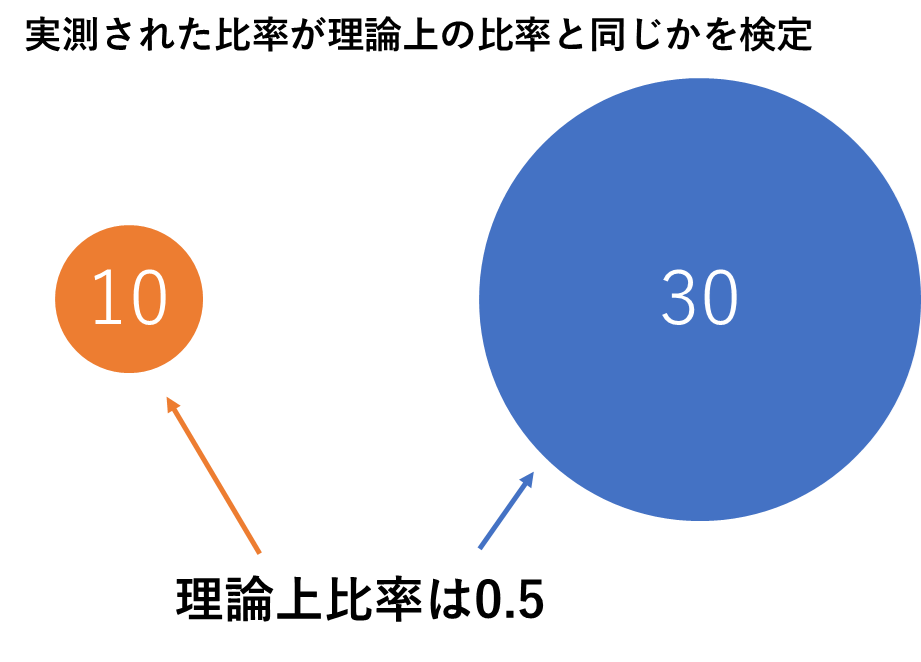
例えば、カテゴリーAとカテゴリーBがあり、カテゴリーAになる確率が理論上 0.5 のとき、AとBの実測値はそれぞれ10と30だった場合を検定すると以下のようになります。
binom.test(c(10,30),n=40, p=0.5)
Exact binomial test
data: c(10, 30)
number of successes = 10, number of trials = 40, p-value = 0.002221
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.1269148 0.4119620
sample estimates:
probability of success
0.25 このようにp値が有意水準0.05を下回っており、有意に0.5からAになる確率は異なっていることになります。
本記事では統計ソフトRを用いた二項検定の方法についてこちらのRのヘルプを参考に紹介します。
二項検定の基本的な方法
二項検定で分析する際に用いる関数は “binom.test()” です。
以下の通りに入力することによって二項検定の結果を出力することができます。
binom.test(検定対象の観測数or2カテゴリーの観測数のベクトル,n=サンプル数, p=理論上の確率)
例Ⅰ)カテゴリーAとカテゴリーBがあり、カテゴリーAになる確率が理論上 0.3 のとき、
カテゴリーAとカテゴリーBの実測値はそれぞれ5と20だった場合
<入力するプログラムコード>
binom.test(c(5,20),n=25, p=0.3)
binom.test(5,n=25, p=0.3)
<出力される結果>
Exact binomial test
data: 5 and 25
number of successes = 5, number of trials = 25, p-value = 0.3829
alternative hypothesis: true probability of success is not equal to 0.3
95 percent confidence interval:
0.06831146 0.40703743
sample estimates:
probability of success
0.2 関数”binom.test()“で利用可能な引数
二項検定で分析する際に用いる関数である “binom.test()”では基本的な引数のほかに以下二つの引数が用意されています。
- alternative・・・両側検定or片側検定を指示(デフォルトは両側検定)
”two.sided”(両側検定)
”greater”or”less”(片側検定) - conf.level・・・信頼区間の範囲を設定(デフォルトは0.95)
使用例は以下の通りです。
例Ⅱ)カテゴリーAとカテゴリーBがあり、カテゴリーAになる確率が理論上 0.3 のとき、
カテゴリーAとカテゴリーBの実測値はそれぞれ25と30だった場合
信頼区間は0.99と設定
<両側検定の場合>
binom.test(c(25,30),n=55, p=0.3,"two.sided",conf.level=0.99)
Exact binomial test
data: c(25, 30)
number of successes = 25, number of trials = 55, p-value = 0.01764
alternative hypothesis: true probability of success is not equal to 0.3
99 percent confidence interval:
0.2831027 0.6340417
sample estimates:
probability of success
0.4545455
<片側検定の場合>
binom.test(c(25,30),n=55, p=0.3,"greater",conf.level=0.99)
Exact binomial test
data: c(25, 30)
number of successes = 25, number of trials = 55, p-value = 0.01108
alternative hypothesis: true probability of success is greater than 0.3
99 percent confidence interval:
0.2977027 1.0000000
sample estimates:
probability of success
0.4545455
binom.test(c(25,30),n=55, p=0.3,"less",conf.level=0.99)
Exact binomial test
data: c(25, 30)
number of successes = 25, number of trials = 55, p-value = 0.9948
alternative hypothesis: true probability of success is less than 0.3
99 percent confidence interval:
0.0000000 0.6181491
sample estimates:
probability of success
0.4545455上記の例のように引数 “alternative” を “greater” と指定すると理論上の確率よりも有意に高いかの検定、”less” と指定すると理論上の確率よりも有意に低いかの検定になります。
(そのため、”less” と指定すると有意にはならないです)
おわりに
本記事ではRを用いた二項検定の方法について紹介しました。
私の記事が皆様のお力添えになれば幸いです。



コメント