生物多様性を表す指数は複数種類あります。
今回はこの指数についてRで算出する方法を記録します。
多様性の3つの考え方
多様性の考え方として以下の三つがあります。
・α多様性・・・ある地域の各地点で考える多様性
→ある地点に生息する種数が多くなるにつれて高くなる
・β多様性・・・ある地域の各地点間の相違で考える多様性
→地点間の差異が大きいほど高くなる
・γ多様性・・・地域全体で考える多様性
→その地域に生息する種数が多くなるにつれて高くなる
これらの考え方の基、さまざまな多様性を表す指標が考えられています。
次章ではその指標についていくつか紹介したいと思います。
優占度を基に計算するα多様性を表す指数
α多様性のもっとも単純な計算方法はその地点に生息する種数です。
しかし、多様性では、それぞれの種が等しく生息しているかを示す均等性も重要であり、単に種数を数えただけでは多様性を完全に示すことができたとは言えません。
そこで、α多様性を表す指数として相対優占度を用いて計算するものがあります。
相対優先度とはある種のその生態系に生息する全個体数に対する割合であり、以下の式で算出します。
・相対優占度=その種の個体数/全体の個体数
この相対優占度を用いて
・シャノン・ウィナーの多様度指数
・シンプソンの多様度指数
を算出することができます。
✓ シャノン・ウィナーの多様度指数
シャノン・ウィナーの多様度指数は以下の式で表されます。

シャノン・ウィナーの多様度指数は 種数が多く、均等度が高いほど値も大きくなります。
自然環境では0.5~3.5の値をとることが多いです
✓ シンプソンの多様度指数
シンプトンの多様度指数は以下の式で表されます。

相対優先度とは言い換えると一個体その環境で生物を採集するとその種を捕獲することができる確率となります。
そのため、その二乗を算出することでランダムに採集した二個体が同じ種である確率を算出することができます。
そしてわかりやすいように1をその値から引く(もしくは逆数をとる)ことでランダムに採集した二個体の生物は同じ種ではない確率となります。
多様度が高いとその確率も高くなり、 シンプトンの多様度指数の値も大きくなります。
Rでの算出方法
renyi関数の利用
先ほど記録した二つの多様性指数について一度に計算することができる関数がveganというパッケージに含まれています。
そのため以下のコードでこのパッケージを呼び起こします。
library(vegan)
多様性指数を計算するためのデータフレームは以下のようになります
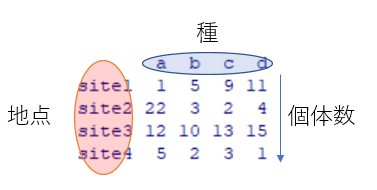
多様性指数の算出はrenyi()という関数を使います。
> exp(renyi(data))
0 0.25 0.5 1 2 4 8 16
site1 4 3.720016 3.509767 3.233345 2.964912 2.756088 2.603164 2.496556
site2 4 3.536570 3.121299 2.485393 1.873294 1.578946 1.479844 1.441678
site3 4 3.989439 3.978972 3.958347 3.918495 3.845314 3.727273 3.582398
site4 4 3.845051 3.703106 3.457979 3.102564 2.725696 2.456217 2.318690
32 64 Inf
site1 2.430015 2.396131 2.363636
site2 1.424766 1.416782 1.409091
site3 3.464111 3.397642 3.333333
site4 2.256673 2.227706 2.200000
指数はexp()を使うことで種数としてみることができ、理解しやすいです。
上記の0は種数、1がシャノン・ウィナーの多様度指数、2がシンプソンの多様度指数を示します。


コメント